Paul Higgs - Research Topics
Population Genetics and Mathematical Biology
This is a rather miscellaneous selection of topics related to population genetics and mathematical biology in general ...
Trypanosomes
1. Tyler, K.M, Higgs, P.G., Matthews, K.R. & Gull, K. (2001) Limitation of Trypanosoma brucei parasitaemia is best described by a combination of density dependent parasite differentiation and parasite killing by the host immune response. Proc. Roy. Soc. Lond. Ser B 268, 2235-2243.
2. Savill, N.J. & Higgs, P.G. (2000) Redundant and non-functional guide RNAs in Trypanosoma brucei are a consequence of multiple genes per minicircle. Gene 256, 245-252.
3. Savill, N.J. & Higgs, P.G. (1999). A theoretical study of random segregation of minicircles in trypanosomatids. Proc. R. Soc. Lond. B 266, 611-620.
The order Kinetoplastida contains some important parasitic species. For example: Trypanosoma brucei is responsible for African Trypanosomiasis, or sleeping sickness; Trypanosoma cruzi causes Chagas' disease; and species in the Leishmania genus cause a range of leishmaniasis diseases. One unusual feature of the group is the kinetoplast DNA in the mitochondrion of the cell. This consists of a network of linked minicircles and maxicircles. The minicircles code for guide RNA sequences that are responsible for editing mRNA transcripts from genes on the maxicircles. We have studied the mechanism of inheritance of minicircles. There are many different classes of minicircle, each of which is present in multiple copies, making several thousand minicircles per cell. When cells divide, segregation of minicircles between cells is not precisely controlled, hence numbers of copies of each type fluctuate considerably. Sometimes minicircle classes can be lost all together, leading to inviable cells. The model predicts that a relatively high proportion of cells are produced that lack essential minicircles, and that there is a selective pressure to increase the size of the minicircle network for this reason. In T. brucei, minicircles usually contain more than one gRNA gene, and there are large numbers of redundant genes and non-functional genes. This is also predicted by our theoretical treatment. [2,3]
T. brucei undergoes a transition from slender to stumpy cell forms in the mammalian bloodstream. The former are proliferative, but the latter are non-proliferative. The transition has been studied experimentally by Keith Matthews, Keith Gull and collaborators in Manchester, and apparently occurs as a response to high cell density. Our work [1] uses a mathematical model to investigate the possible mechanisms by which this transition could occur.
Memes - how ideas spread
P.G. Higgs. The Mimetic Transition - a simulation study of the evolution of learning by imitation. Proc. Roy. Soc. Lond. Ser. B 276, 1355-1361 (2000).
A meme is an element of culture that can be passed on by imitation. Memes can be trivial (e.g. catchy tunes), or can have huge influence (e.g. religious faiths). Memes can be abstract (e.g. the principle of democracy) or down-to-earth (e.g. stone axes). Culturally transmitted ideas and skills must have influenced the ability of our ancestors to survive and bring up children. Susan Blackmore, in her recent book 'The Meme Machine', proposed that memes can explain why we have such big brains: brains evolved because of selection for the ability to imitate. Individuals with genes that confer a better ability to learn by imitation are more likely to acquire memes that increase their fitness, and hence are more likely to pass on their genes. I have been working on a mathematical model to test this idea. The model shows that genes for increased learning ability are selectively favoured. The mean learning ability of the population increases slowly until a mimetic transition is reached where the memes become able to spread like an epidemic. At this point there is a dramatic increase in the number of memes known, the mean fitness of the population, and the mean learning ability. The model also shows that selection in favour of imitation is sufficiently strong to overcome negative selective effects on large brain size due to increased energy requirement and possible difficulties at childbirth.
A population genetics model for multiple quantitative traits
C.F.Taylor and P.G. Higgs. A population genetics model for multiple quantitative traits exhibiting pleiotropy and epistasis. J. Theor. Biol. 203, 419-437, (2000).
This work concerns the role of pleiotropy (where genes have multiple effects), and epistasis (where a gene's effect depends on its genetic 'background'), in evolution and speciation. The model simulates organisms with a variable number (T) of quantitative traits, the value of each being dependent on a number of loci (L) picked at random from the organism's genome of Ltot loci.
If LT << Ltot then the sets of loci linked to the different
traits rarely overlap; traits may evolve independently, and genotypes are
possible which simultaneously optimise all traits.
If LT >> Ltot there will be many loci affecting multiple traits; in
general this means that it is impossible to find a genotype which optimises all
traits, resulting in a rugged fitness landscape. This means that there are many
different 'answers' to the 'question' posed to organisms by selection.
The MQT model
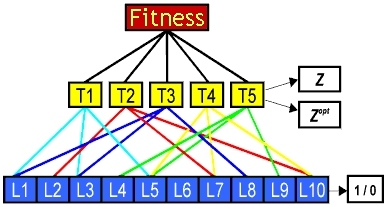

We have studied the fitness
landscapes generated by this model, using exhaustively enumerative, adaptive
walk based, and population based approaches. Since genotypes of populations can
change easily, isolated populations will diverge in genotype even if they are
under the same selective forces. We are now looking at the effects of
hybridisation on the fitness of individuals using our quantitative trait model.
We consider crosses between two sub-populations of the same species that have
evolved separately with the same selection on the phenotype. The typical
situation is that F1 hybrids have a slightly increased fitness with respect to
the parent populations, whereas F2 individuals usually have a considerably
decreased fitness because of the break-up of co-adapted complexes of genes. Low
hybrid fitness leads to a barrier for gene flow between populations.
Some older publications in the Population Genetics Area
1.
P.G.Higgs and
B.Derrida. Stochastic Models for Species Formation in Evolving Populations.
J.Phys.A (Math. & Gen.) 24, L985, (1991)
2.
P.G.Higgs and
B.Derrida. Genetic Distance and Species Formation in Evolving Populations. J.
Molecular Evolution 35, 454, (1992).
3.
P.G. Higgs.
Error Thresholds and Stationary Mutant Distributions in Multi-locus Diploid
genetics models. Genetical Research (Camb) 63, 63, (1994).
4.
P.G.Higgs and
G.Woodcock. The Accumulation of Mutations in Asexual Populations, and the
Structure of Genealogical Trees in the Presence of Selection. J. Math. Biol.
33, 677-702, (1995).
5.
P.G.Higgs.
Frequency Distributions in Population Genetics Parallel those in Statistical
Physics. Phys. Rev. E 51, 95, (1995).
6.
G.Woodcock and
P.G.Higgs. Evolution on a Multiplicative Single-Peak Fitness Landscape.
"Advances in Artificial Life" Eds. F.Moran et al Lecture Notes in
Artificial Intelligence no. 929, p 148, Springer (1995).
7.
G.Woodcock and
P.G.Higgs. Population Evolution on a Multiplicative Single-Peak Fitness
Landscape. J. Theor. Biol. 179, 61-73, (1996).